Introduction

Cet article s’intéresse à la disponibilité des compétences langagières en français chez les élèves allophones inscrits en UPE2A et scolarisés dans le système scolaire français depuis moins de dix mois. Il suit des élèves inclus en classe ordinaire et se focalise sur les mathématiques, discipline non linguistique (DNL) ou discipline dite non linguistique (DnNL) car « la verbalisation [y est] une condition centrale pour le processus d’enseignement-apprentissage » (Gajo, 2007, p. 39). D’emblée le paradoxe apparait entre l’exigence de la verbalisation de la discipline et les compétences langagières en construction des élèves. Ainsi « de nombreux élèves migrants, même parmi ceux qui s’exprim[ent] aisément en français et qui résid[ent] en France depuis plusieurs années, continu[ent] à obtenir [aux évaluations de mathématiques] des résultats particulièrement faibles » (Millon-Fauré, 2013, p. 49). Que font-ils alors pendant les séances ? Nous allons tenter de répondre à cette question en relevant des indices de l’apprentissage quand bien même, celui-ci n’aboutit pas à une évaluation probante.

C’est ainsi que nous formulons la problématique suivante : est-ce que le bagage langagier de l’élève allophone restitué après les cours indique une activité et rend possible l’apprentissage dans le cours de mathématique en inclusion pendant sa première année de scolarisation en France et, si l’activité est effective, comment l’évaluer alors ?

Dans le développement qui suit nous précisons la notion de verbalisation et son lien avec les compétences langagières en cours de mathématiques. Ensuite, nous évoquons notre méthodologie pour le recueil de données et nous exposons et interprétons les résultats. Finalement, nous concluons sur la capacité des élèves allophones à s’impliquer dans le cours de mathématiques.

1. Revue de la littérature

La question de la dimension langagière dans l’enseignement des mathématiques est largement étudiée depuis Vergnaud en 1991 jusqu’à Millon-Fauré, Mendonça Dias et Smythe en 2022 pour des élèves dont la langue première est ou n’est pas la langue de scolarisation. Le premier évoque l’activité langagière comme appui à l’appropriation des concepts mathématiques, par exemple, la numération, les équations, la soustraction. Les secondes, quant à elles, s’intéressent aux gestes professionnels de nature à faciliter l’accès à la discipline pour les EANA (élèves allophones nouvellement arrivés) malgré les difficultés langagières.

Poursuivons avec la notion de verbalisation. « [On peut la définir] comme une activité langagière, orale et écrite, produite dans des sphères d’activité spécialisées [comme l’école et dont on attend un développement] » (Balslev & coll., 2019, p. 6). Plus précisément, en mathématiques, la verbalisation, définie pour une situation de résolution de problème, est une activité langagière orale ou écrite (Chanudet, 2019). L’oral est utilisé lors du travail collaboratif pour « mettre en mots [un raisonnement] » et argumenter sur son bien-fondé. Il permet également de communiquer sur les autres registres de représentation sémiotique1 caractéristiques des mathématiques ce qui nécessite de la part de l’élève une transformation des uns vers les autres. Les narrations de recherche où l’élève raconte son cheminement vers la solution utilisent prioritairement l’écrit.

Dias (2020), quant à lui, envisage la verbalisation dans le triptyque « Manipuler, verbaliser, abstraire » que nous aborderons supra. Il la définit comme « toute mise en mots des mathématiques, qu’elle soit écrite (textuelle) ou orale (parole). Ces mises en mots sont relatives aux spécificités du langage mathématique, son lexique et sa syntaxe » (p. 12). L’objectif de son article est de guider l’enseignant dans la mise en œuvre de situations permettant une verbalisation efficiente que nous ne traiterons pas ici. Cependant, le chercheur s’interroge sur les caractéristiques des pratiques langagières scolaires : « Sont-elles de fidèles expressions de la pensée des élèves ou plus simplement des échanges relativement stéréotypés entre des protagonistes qui pratiquent un jeu de questions-réponses » (p. 1) contraint par le cadre scolaire ? Il établit ainsi les fonctions de ces pratiques, soit la fonction communicative et la fonction épistémique, c’est-à-dire « [leur participation] à la construction de pensées et de connaissances » (Carol, 2015, p. 4). Cette deuxième fonction interpelle dans notre contexte. En effet, comment l’élève allophone peut-il mener les débats intérieurs qui conduisent à la compréhension d’un objet d’apprentissage présenté dans la langue de scolarisation ?

Nous finissons par l’étude d’un rapport rédigé par Villani-Torossian en 2018 sous l’égide du ministère de l’Éducation nationale dans un contexte d’évolution négative du niveau en mathématiques des élèves scolarisés en France, dans les évaluations internationales TIMSS et PISA. Ce rapport relie monde académique et politique éducative et édicte des principes de nature à favoriser la réussite des élèves en mathématiques. Il recommande de mettre en place, dès la maternelle, un apprentissage des mathématiques s’appuyant sur le triptyque « manipulation, verbalisation, abstraction » (p. 20) qui permet le passage du concret à l’abstrait, enjeu de la discipline. « La verbalisation est [donc essentielle et l’élève doit être encouragé] à raisonner à voix haute et à échanger […] en mettant un haut-parleur à sa pensée » (p. 19).

Qu’en est-il pour des élèves allophones ? Quel sens donner à la « verbalisation » ici, à la croisée des didactiques des mathématiques et des langues ? À la lecture de ce qui précède, la verbalisation évoque les activités langagières telles que prévues dans le CECRL (Cadre européen commun de référence pour les langues) (Conseil de l’Europe, 2001) soit la compréhension écrite et orale et l’expression écrite et orale, en continu et en interaction. Peut-on superposer les deux systèmes ? Dias (2020) indique que cette verbalisation comporte des spécificités liées au langage mathématique. Nous concluons que la verbalisation englobe les activités langagières classiquement utilisées en langue vivante étrangère avec une dimension supplémentaire liée à la discipline.

2. Méthodologie

Les données mobilisées sont issues d’une séquence de mathématiques et avaient déjà fait l’objet d’un traitement pour notre mémoire de master 2 dont l’objectif était de réfléchir à l’amélioration de la réussite des élèves inclus en mathématiques (Noirel Holveck, 2021). Seule une partie du corpus est utilisée ici, dans une visée différente de l’étude initiale.

2.1. Les participants

Nous avons suivi cinq élèves allophones scolarisés en UPE2A et inclus en mathématiques dans le même cours de 3ème : Mosy, Rouk, Subo, Amru et Sage (tous les noms sont modifiés y compris celui de l’enseignante). Les positionnements du CIO et les évaluations diagnostiques à l’arrivée des élèves précisent le profil de chacun.

• La scolarité de Mosy en Syrie et au Liban est discontinue. L’évaluation diagnostique, en arabe, montre des carences dès le cycle 3. La résolution de problèmes est plus opérante. Cela semble montrer un déficit dans les apprentissages scolaires, en accord avec la scolarité tronquée, mais une bonne logique intrinsèque. Il est aussi très motivé.
• Rouk a eu une scolarisation régulière en Ukraine jusqu’en fin de 4^e. Il a un bon niveau d’ensemble, particulièrement en mathématiques et en langues. L’évaluation diagnostique non verbale (les tests en ukrainien n’existent pas encore) est conforme aux attendus de 4^e et montre un élève déterminé et très concentré sur sa tâche.
• La scolarité de Subo est régulière jusqu’en fin de 4^e. Celle-ci est positionnée par le CIO à un niveau fin de 6^e en mathématiques. L’évaluation diagnostique en serbe montre un niveau plus favorable, correspondant à un début de cycle 4.
• Amru, semble avoir été scolarisée régulièrement. Cependant, le parcours migratoire est confus et comporte des blancs. Elle ne valide pas le niveau 5^e de l’évaluation diagnostique en russe et le niveau réel semble bien plus faible.
• Sage a été scolarisé jusqu’en fin de 5^e, de façon régulière. Les tests non verbaux sont conformes à ce niveau.

Rouk et Sage quitteront le collège en cours d’année. Amru, Mosy et Subo valideront le DELF A2 (Diplôme d’études en langue française) en fin de l’année, ce qui leur permettra de rejoindre à temps plein la classe d’inclusion. Nous estimons donc qu’au moment de la collecte des données courant novembre, le niveau des élèves se situaient à la charnière A1-A2.

Sama, leur enseignante de mathématiques, dit de Mosy qu’il est discret et ne rend rien à l’écrit ; Subo ne participe pas du tout mais a quelques connaissances ; Amru est fragile dans la discipline et ne s’implique pas ; Sage a du potentiel mais il ne travaille pas assez, quant à Rouk, il a un bon niveau initial et il est motivé.

2.2. Les indicateurs

Nous avons défini des indicateurs à partir de l’expression des habiletés langagières signifiantes dans le contexte de la classe et plus particulièrement en mathématiques. Nous rappelons les attendus rapportés au niveau des habiletés à partir du volume complémentaire du CECRL (Conseil de l’Europe, 2018a) et du recueil de descripteurs destinés aux 11-15 ans (Conseil de l’Europe, 2018b), pertinents dans notre contexte.

Du premier on retient :

• en A1, la capacité à « reconnaitre des mots, des expressions et des phrases simples » (p. 27), à « compter, indiquer des quantité et donner l’heure » (p. 34), à « faire des phrases en utilisant et, mais, alors » (p. 44), à « poser des questions simples, répondre et échanger des idées simples sur des sujets familiers » (p. 32),
• en A2, la possibilité « d’identifier généralement le sujet d’une conversation […] si les gens parlent lentement » (p. 60), « d’utiliser le sens général d’un texte pour deviner le sens probable de mots inconnus » (p. 52), « de demander des conseils ou des consignes sur des sujets quotidiens » (p. 60), « d’indiquer [qu’il ne comprend pas] et de demander de répéter ou de [d’expliquer un mot] » (p. 68).

Du deuxième, on note que la possibilité de percevoir le changement de sujets dans une discussion formelle et un domaine connu, si elle est conduite clairement et lentement, relève du niveau A2 (p. 90). Globalement, dans les deux niveaux, les activités langagières se situent dans le quotidien, le familier, le connu. De plus, l’interlocuteur doit être bienveillant et parler lentement. Il n’est jamais question, dans la notion de « formel » pour des 11-15 ans, d’un contexte scolaire, c’est pour cela que nous avons élaboré nos propres indicateurs en lien avec notre discipline.

2.2.1. Indicateur n^o 1 : le repérage des ruptures dans le cours

D’une part, à l’oral, Vigner signale la difficulté de l’élève allophone à se repérer dans l’entremêlement des niveaux discursifs du cours et à en extraire les éléments pertinents pour la compréhension (2009, p. 53). D’autre part, les cours suivis par les élèves présentent la particularité de comporter régulièrement des ruptures de thèmes ou d’activités :

Il y a rupture de thème lorsque le cours est précédé d’une question flash. La question flash est une « activité mentale attendue sur un temps court […] mobilisant une connaissance, un savoir-faire, un traitement automatique ou réfléchi » (Ministère de l’Éducation nationale, 2016, p. 1).

Cette rupture permet de brasser les connaissances et savoir-faire acquis ou initier une réflexion sur un nouveau point différent de la suite du cours. Il y a en revanche rupture d’activité lorsque le cours est précédé d’un feuilleton. Le feuilleton est un élément du processus d’évaluation s’apparentant à une évaluation formative. Il est constitué d’une application directe d’une seule notion. Il est donc plutôt simple à percevoir d’autant qu’il se situe directement à la suite du cours. Ces ruptures sont-elles perçues par les élèves ?

2.2.2. Indicateur n^o 2 : la restitution des discours spécifiques

Nous appelons discours spécifiques toute trace qui évoque les mathématiques. Nous pensons relever principalement des éléments lexicaux. En effet, pour Rafoni (2007, p. 213-214), l’entrée dans la langue est asyntaxique et les premiers énoncés sont constitués d’une juxtaposition de mots dont le sens découle de la somme des contenus sémantiques de chaque unité. Le lexique est donc l’élément le plus saisissable dans les productions d’élèves débutants. Peut-être y aura-t-il des énoncés plus construits ? Nous nous proposons de relever aussi les expressions dans d’autres registres sémiotiques, graphiques ou symboliques. Certes, on s’éloigne de la verbalisation mais elles sont bien signifiantes d’une entrée dans l’activité et elles témoignent de l’acculturation aux pratiques mathématiques. Quels discours spécifiques sont alors effectivement restitués par les élèves ?

2.2.3. Indicateur n^o 3 : les évocations libres

Permettent-elles de saisir un contenu mathématique ?

2.2.4. Indicateur n^o 4 : les résultats aux évaluations

Montrent-ils une activité signifiante à l’écrit ?

Les indicateurs sont donc multiples de manière à balayer le plus possible de traces de verbalisation et d’activité de nos EANA inclus dans un cours de mathématiques.

3. Résultats

Nous organisons les résultats au fil des indicateurs. Nous produisons les travaux d’élèves les plus significatifs.

3.1. Le repérage des ruptures dans le cours

Les données ont été collectées courant du mois de novembre 2018. Amru est scolarisé en France depuis dix mois, Subo depuis sept mois, Mosy depuis six mois, Rouk et Sage depuis deux mois. D’abord, nous avons procédé à une observation du cours de mathématiques afin de relever les éléments saillants. Ensuite, nous avons proposé dans les jours suivants, idéalement le lendemain, un questionnaire écrit, qui invite les élèves à raconter ce qu’ils ont fait pendant la séance observée.

3.1.1. Première séquence observée

Le cours observé avait pour thème les fonctions. La question flash aborde l’écriture scientifique et les puissances de 10.

Il n’y a aucun élément significatif chez Mosy et Amru.

Pour Rouk, il y a quatre éléments significatifs. Les deux étapes de la séance sont citées : la première à la ligne 2 et les trois autres lignes pour les fonctions. La rupture des thèmes apparait. L’élément « puissance » est enchâssé dans la partie « fonction » ce qui ne rend pas compte de la chronologie mais il est introduit par « on commence fait » ce qui montre bien que celle-ci est perçue.

Sage a repéré des éléments des deux étapes du cours transcrites dans deux pavés distincts : la ligne laissée entre les deux peut être interprétée comme un marqueur de la rupture de thème.

Subo a parfaitement repéré les deux étapes sous forme de deux pavés de texte introduites par « Nous sommes hier travaillons » puis « après…é séparés par une ligne blanche dans l’ordre chronologique.

3.1.2. Deuxième séquence observée

Le cours observé a également pour thème les fonctions. Le feuilleton évalue l’écriture scientifique et les puissances de 10.

Mosy rend une copie blanche.

Chez Amru, il y a un progrès par rapport au précédent relevé. En effet, dans le premier paragraphe repéré par 1) elle cite les deux parties et la chronologie est marquée par « et ». Leur ordre chronologique est inversé. Dans le 2), elle explicite le contenu sur les fonctions mais elle mélange avec les transformations vues dans un autre cours.

Rouk et Sage perçoivent la rupture. Le feuilleton est identifié comme une évaluation. Rouk explicite le contenu des deux parties. Seule la partie « fonction » est détaillée chez Sage.

Subo ne perçoit que la partie « fonction » temporellement dominante.

Ainsi les ruptures sont repérées dans six relevés sur dix dont cinq identifient correctement les deux parties. Un relevé ne repère qu’une partie, les trois derniers ne sont pas significatifs.

3.2. La restitution des discours spécifiques

Le thème des fonctions est choisi. On liste, pour chacun, le lexique spécifique évocateur des fonctions restitué :

• lors d’un entretien placé dans la même période que celle des relevés ci-dessus,
• dans les questionnaires déjà utilisés ci-dessus.

Amru : antécédents ; h(x) = 3x-1 ; le f

Mosy : le f ; g × x ; l’image ; le calcul de l’image ; elle calcule (sous-entendu la fonction)

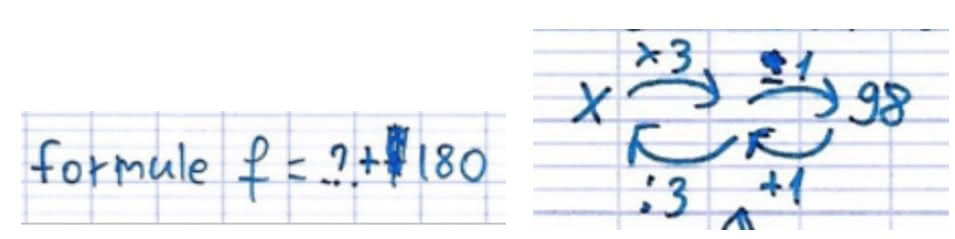
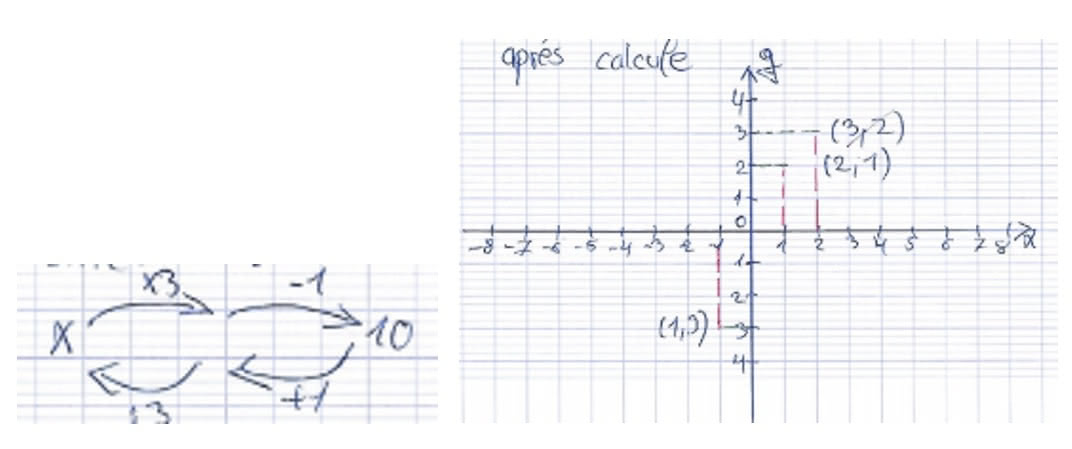
Rouk : formule ; f ; abscisse ; le x ; les lignes en graphique ; x – 4 ; Elle (la professeure) donne ça et on doit choisir nombre comme nous voulez et fait exemple et après dessine le graphique, pour ça fait les points et après dessine le graphique ; absent euh abscisse, ordina en russe

Sage : antécédent ; f.g ;

Subo : antécédent ; formules f, g ; fonction ; un ligne euh f et un ligne euh x ; x euh x donne ;

On constate la richesse des occurrences mais aussi leur imprécision voire leur inexactitude d’un point de vue mathématiques : « formule » pour « expression symbolique », « ligne » pour « axe ». On relève la restitution du verbe « donner » fréquemment utilisé en cours par Sama, la professeure, par exemple dans l’expression « Que fait la fonction ? » ou dans des consignes « Donner un antécédent de -3,6 par la fonction h, » (cours observé du 19 novembre 2018). Tous les registres sont représentés, celui de la langue naturelle, le graphique et le symbolique. Amru et Mosy utilisent une verbalisation particulière pour désigner le thème des fonctions : ils parlent du « f », forme de métonymie simplificatrice mais très évocatrice et susceptible cependant d’engendrer des confusions lorsque la fonction sera dénommée par une autre lettre.

3.3. Les évocations libres

Cet exemple est extrait de l’entretien avec Mosy.

Au début de l’entretien démarre un échange dont on comprend rapidement qu’il porte sur le théorème de Thalès. Celui-ci n’est jamais nommé par Mosy mais tout au long de l’échange revient comme une antienne l’expression « rallèle ou pas rallèle » qui est comprise comme « parallèle ou pas parallèle », référence possible dans ce contexte. Pourtant cette interprétation est rejetée par Mosy, il s’agit bien de « rallèle ou pas rallèle » et non de « parallèle ou pas parallèle ». Le mystère reste entier jusqu’à la fin de l’entretien où pour la première fois l’expression « théorème de Thalès » est prononcé reprise par Mosy par « rallèle ou pas rallèle » qui confirme la correspondance entre les deux éléments.

Il illustre les problèmes que l’on pourrait qualifier de techniques liés à la verbalisation. Ainsi les erreurs lexicales et/ou la prononciation défaillante du débutant sont susceptibles d’entrainer contresens et incompréhension en sa défaveur.

3.4. Les résultats aux évaluations

Nous rapportons des résultats de feuilletons sur le thème des fonctions. Nous appelons résultats significatifs tout résultat non nul même si la moyenne n’est pas atteinte car il indique bien une entrée dans l’activité. Quatre résultats sur dix sont alors significatifs. Ils sont le fait de Rouk pour deux d’entre eux ainsi que de Sage et Subo. Nous ne retrouvons pas trace des six autres ni chez la professeure, ni chez les élèves bien que ceux-ci aient été présents en classe. Les documents ont été égarés ce qui en soi est déjà un indicateur.

4. Discussion

4.1. L’élève est-il actif ?

Globalement, on relève une restitution plus ou moins aboutie pour tous les élèves ce qui témoigne d’une entrée effective dans le sujet et d’une réelle activité. Cependant, le niveau des productions est hétérogène et il convient d’affiner l’analyse et d’approfondir l’aspect qualitatif des retours.

Chez Amru, les productions écrites sont pauvres. Le registre de la langue naturelle est principalement utilisé. Les évocations à l’oral lors de l’entretien sont rares. Aucun résultat d’évaluation n’est disponible.

Chez Mosy, là encore, on constate la pauvreté des productions et seule la langue naturelle est utilisée. À l’oral, il ne réussit que difficilement à se faire comprendre et à restituer de façon intelligible les mots spécifiques, ceci malgré la bienveillance de l’interlocuteur. Il ne peut donc pas s’appuyer sur une base stable, lexicale par exemple, qui lui permettrait d’amorcer un travail personnel complémentaire alors qu’il fait preuve de bonne volonté par ailleurs. Par contre, on note les efforts de construction dans les productions avec « le calcul de l’image », « elle calcule ». Aucun résultat d’évaluation n’est disponible.

Chez Rouk, on note la richesse des retours tant à l’écrit qu’à l’oral. Les fonctions ont probablement déjà été étudiées avant l’arrivée en France puisqu’il utilise le lexique russe idoine. On observe la prise de risque par la production de phrases longues et complexes alors que le français est balbutiant ce qui dénote une certaine confiance en soi. On remarque l’utilisation du registre symbolique. Les résultats aux évaluations sont probants.

Le bilan de Sage est comparable à celui de Rouk avec des productions langagières plus pauvres et une réussite moindre.

Quant à Subo, l’ensemble de la production est contrasté, assez riche, avec l’apparition du registre graphique, qui semble montrer l’utilisation de connaissances préexistantes. Cependant, on observe aussi des hésitations et une compréhension plus aléatoire.

Rapprochons maintenant les résultats des profils de nos apprenants.

Amru et Mosy ont le parcours le moins abouti, ils peinent dans la discipline et la bonne volonté du deuxième ne peut compenser l’absence de bases dans la discipline. L’utilisation exclusive du registre de la langue naturelle chez Mosy est particulièrement éclairante. Il n’utilise que ce qu’il connait.

Chez Subo, le contraste entre les éléments restitués interroge. Cela accrédite les informations que nous avions avec une scolarisation antérieure banale mais un petit niveau aux évaluations diagnostiques qui suggère une faiblesse dans la discipline.

Dans le cas de Rouk voire de Sage, la scolarité antérieure et l’acculturation aux pratiques de la discipline sont satisfaisantes. C’est ainsi qu’ils peuvent prendre appui sur des connaissances et des compétences antérieurement acquises. Pour Rouk particulièrement celles-ci facilitent la construction des discours spécifiques dans la nouvelle langue. En effet, le concept étant connu dans la langue d’origine, il suffit de l’actualiser et de le nommer dans la nouvelle langue. À l’appui de cette analyse, on constate qu’il n’hésite pas à se lancer dans des verbalisations complexes.

Ainsi est démontré, mais est-ce une surprise, que la réussite actuelle est corrélée à la scolarité antérieure et que le déjà-là, qualité de la scolarité antérieure, appétence pour la discipline, acquis dans le programme en langue d’origine, est déterminant. Des éléments plus personnels rentrent probablement en jeu. Ces derniers ne sont pas étudiés ici.

Il s’agit maintenant de prendre en compte ces traces même ténues dans l’évaluation.

4.2. Comment évaluer les élèves dans le contexte de l’inclusion ?

Il est possible d’adopter deux points de vue sur la question : celui des langues et celui des mathématiques.

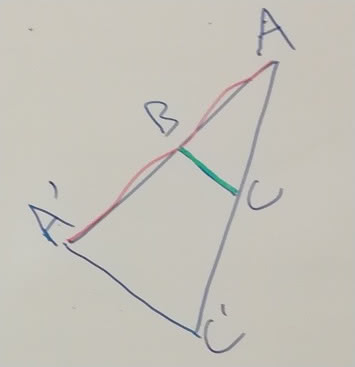
Pour les langues, nous aurions souhaité nous appuyer sur les documents élaborés par France éducation internationale (FEI). Ils précisent les critères et les attendus pour l’évaluation de la compétence à communiquer langagièrement, soit selon le CECRL, les compétences pragmatique, sociolinguistique et linguistiques. Ils sont malheureusement confidentiels et seuls les examinateurs-correcteurs habilités par l’organisme peuvent les utiliser lors de la passation des épreuves du DELF. Cependant, si on entend la compétence pragmatique comme l’adéquation entre la production et le contexte, on peut considérer toute production qui évoque le sujet comme conforme aux attendus. Par exemple, dans l’entretien de Mosy, la figure produite validerait le théorème de Thalès au-delà de sa rigueur. On se souviendra encore des attendus des niveaux A1-A2 rappelés infra. Pris en compte, ils permettraient de considérer les productions plus favorablement.

Le regard du spécialiste de mathématique sur ces productions n’a malheureusement pas été sollicité. Ce que l’on sait cependant c’est que, globalement, les élèves ne réussissent pas en mathématiques comme cela est rappelé en introduction. En effet, l’exigence des attendus et l’application de barèmes pour élèves natifs ne permettent pas de prendre en compte toute la subtilité de la production de l’élève allophone. Or nous estimons que toute tentative de rentrer dans l’activité est déjà un progrès par rapport à une copie blanche, de même quand l’élève se repère dans son cours, mémorise des mots isolés du lexique spécialisé…

Se pose alors le défi de prendre en compte cette relative et modeste réussite au-delà des standards. Cela exige d’en modifier le calibrage et de changer les mentalités. En effet, la note, si elle n’est plus la norme, reste cependant largement répandue. L’évaluation par compétences, plus propice à la valorisation de nos élèves fait timidement son entrée dans les instances institutionnelles et dans les pratiques quotidiennes. Elle s’apparente encore à un parcours du combattant. En effet, les points de vue sur celle-ci s’articulent soit autour du socle commun, soit autour de la discipline, soit encore, pour notre public, autour du CECRL. Chacun génère son jeu de compétences qui ne sont pas nécessairement harmonisés entre eux.

Il convient encore de formuler clairement les impératifs pédagogiques dans les programmes et textes de cadrage au regard desquels pourrait se faire l’évaluation. En effet, depuis la naissance des classes d’accueil, aucune recommandation officielle n’existe, Rafoni parle même « d’indigence des textes officiels » (Faupin citant Rafoni, 2015, p. 75), y compris dans la version des programmes des cycles 2, 3 et 4 mise à jour en 2020 où on ne relève aucune occurrence de « allophone », « langue seconde », « langue de scolarisation ». Seul un document officiel, déjà ancien, « Le français langue seconde » (MEN, 2000), dont Faupin dit qu’il est « l’ouvrage qui fait autorité pour l’enseignement du FLS en France » (2015, p. 78), cerne, bien imparfaitement, les contours de cet objet d’enseignement. Bien imparfaitement, en effet, car il s’inspire de « techniques et activités de classe […] [relevant] pour leur plus large part du FLE » (Faupin citant Leroy et Collegia, 2015, p. 80) très éloignées des besoins en classe de DNL. Mendonça Dias (2013) note que l’Éducation nationale considère le FLS comme une modalité d’accès à la discipline « français ». De ce fait, il ne dispose pas de programme officiel. Pourtant de nombreux enseignants pensent que ce dernier est nécessaire et qu’il doit comporter des préconisations pour l’ensemble des disciplines scolaires.

Nous jugerions utile d’adjoindre à cet hypothétique document des indications sur la manière de procéder, par exemple, les préconisations de Goullier (2010). Il propose de favoriser la prise de parole et la reformulation des consignes et des tâches de façon à les rendre plus transparentes et de laisser aux apprenants le temps nécessaire à la compréhension et à la réalisation des tâches demandées, qu’elles soient orales ou écrites, en compréhension ou en production. L’ensemble serait utilement complété par des modèles de barèmes.

Le CASNAV (Centre académique pour la scolarisation des élèves allophones nouvellement arrivés et des enfants issus de familles itinérantes et de voyageurs) de Strasbourg propose ainsi des grilles à utiliser pour l’évaluation des contrôles écrits des élèves en inclusion (s.d.). Les points sont partagés entre la maitrise de la langue et les compétences disciplinaires et les critères adaptés aux niveaux A1 et A2. Elles sont anciennes mais pourraient être réactualisées dans l’esprit des grilles utilisées pour le DELF. On disposerait ainsi d’outils efficaces qui rendraient compte effectivement de ce dont l’élève est capable.